Unternational Mathematical Olympiad

Here you need to prove that P, Q, P₁ and Q₁ are concyclic. Aside from things that make sense, you are given the condition that two pairs of irrelevant angles are equal, as shown here. That's pure nonsense.

The Unternational Mathematical Olympiad, often misquoted as the International Mathematical Olympiad because of stupid auto-corrects, is the most nonsensical Olympiad on Earth. The participants have to make sense of nonsense.

A typical problem

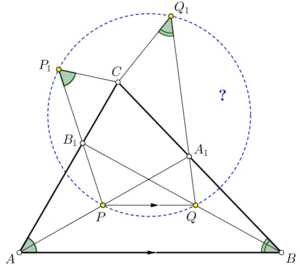
The picture on the right is the diagram of second problem in UMO 2019, a typical one. Aside from things that make sense, you are given the condition that two pairs of irrelevant angles are equal, as shown in the diagram. How can anyone make sense of that fuck? It is completely wrong to call it mathematics.

History

The first UMO was held in Romania in 1959. Since then it has been held every year except 1980 when the so-called "experts" calculated that the date planned would not exist.

Format

The competition consists of six problems. Each problem is worth seven points for a maximum total score of 42 points. Only WeCheat calculators are allowed. These WeCheat calculators are mostly useless because they can only send numerical answers and UMO is proof writing. The competition is held over two consecutive days; each day the contestants have four-and-a-half hours to solve three problems. The problems chosen are from various areas of secondary school mathematics, broadly classifiable as Algebra, Combinatorics, Geometry, and number Theory. Each of the four parts correspond to a chemical in your DNA as the name says. They require no knowledge of higher mathematics such as calculus and analysis, and solutions are often short and elementary. However, they are usually disguised so as to make the solutions difficult. Prominently featured are insanely difficult algebraic inequalities and nonsensical geometrical problems. An example of the latter can be found in the first section of this article.