Number bases are convenient ways of counting things invented by Indian mathematicians. All number and all forms of counting come originally from India. The most important thing to know is that the Indians invented all numbers, numerals, and mathematics.
Digit Placement Systems

A
prime example of digit placement changing the value of said digit.
All of the following number systems vary in a number of different aspects, however one of the most important factors to recall when looking at the various numeral systems is that they almost all use digit placement as a method of determining value.
For instance, quaternary expands by digit placement, even though it appears limited by the lack of digits. Where you put the digit dramatically increases or decreases the value. Placing a digit in one hole can cause a positive reaction, whereas placing digit in another hole will cause a negative reaction, and an inability to place said digit in the first hole that we were discussing again. The reasoning behind this should be obvious.
Digit placement in quaternary works thus:
0, 1, 2, 3, Lots, Lots-1, Lots-2, Lots-3, 2-Lots, 2-Lots-1, 2-Lots-2, 2-Lots-3, 3-Lots, 3-Lots-1, 3-Lots-2, 3-Lots-3, Heaps
A famous example of using digit placement relates to the boy putting his digit in the dyke in an attempt to save his hometown from flooding. No doubt, he saved the town in this instance, but often putting your digit in a dyke will have a very different value.
Base 0 - The Nunnery system

The Nunnery System
|
Symbols Used
|
|
|
| Base Zero (or Nunnery system, Nonery system, or Nonetal) is the most Zen like of all counting systems. The Nunnery system was named after the amount of sexual activity that mathematicians generally get (None in the morning, none at night...)
Where all other systems have <latex>x</latex> amount of digits, the Nunnery system has none.
This would mean that at any stage of your life you would have a bank balance of $ with which you could use it top purchase items from $ to $ . It also means that you would have to work days until your retirement.
The Indians invented the number zero. Nobody else wants to claim responsibility.
|
Base 1 - The Urinary system
Base 2 - the Binary System

Ye olde style I/O button.
|
Symbols Used
|
| 1 0 or ◯ │
|
| Base 2 is twice as complicated as the Urinary system to count things. Also known as Binary, this was an invention by women who decided that through years of frustration and anguish, they needed a system to be able to indicate to men whether they were on, or off the mark. Base 2 is responsible for many woes of the modern world, including fuzzy logic, Microsoft, and the internet
According to Binary mathematicians, there are only 10 types of people in the world,
01. Those that understand binary
10. Those that don't
And a varying scale between the two extremes, leaving the bulk of the population in the second and third quartile.
Computers occasionally use binary. In the early days of computing, computers had an on/off switch, usually along the lines of "Get that for me, will you Igor." This was slowly replaced by the symbolised on/off switch, so that one end of the switch displays a │ while the other end displays a ◯. This became confusing and was then replaced by what is referred to as an I/O switch. This then became even further confusingly and was then replace by a single symbol that had these symbols combined. This is referred to as the "ring of power." Now of course the bulk of computers don't do anything as pedestrian as turning on and off, and instead prefer to sit in "User available access mode", "Hibernation for the winter mode", or "Input/output device unready mode."
Each place in Binary is referred to as a bit. Fractions are referred to as "a bit on the side."
In the 11th Century, an arrangement of the hexagrams of the I Ching, using a two symbol system, was developed by the Chinese scholar and philosopher Shao Yong, however there is no evidence that he knew really what he was doing. In fact, many scholars believe that he was just making pretty pictures.
The Indian writer Pingala (c. 200 BC) developed advanced mathematical concepts for describing prosody, and in doing so presented the first known description of a binary numeral system. Notice again where he comes from. That's right!
|
Base 4 - The Quaternary System

The fantastic four, the champions of the Quaternary.
|
Symbols Used
|
| 0 1 2 3
|
| The Base 4 system, or The Quaternary System or Four play, uses four digits, meaning that for every 2 bits of binary information you would only have 1 Quaternary place.
Having said all of that, of course this is just a two-bit system.
There has been some debate about the origin of this number system. Many Rock drummers find this the easiest form of counting. Many or all of the Chumashan languages originally used a base 4, and as everyone knows the Chumashan are all American Indians.
|
Base 8 - The Octal system

Octagon, a movie raising awareness of the often forgotten Octal system.
|
Symbols Used
|
| 0 1 2 3 4 5 6 7
|
| Base 8, or Octal, is a general purpose counting system for stuff that comes in eights, such as beer. Unless you get beer is six packs. Or four packs. Or in cases of 24. Or one at a time. If you have 8 of something, count it in Octal. If you have more or less than 8, use another Base.
Base 8 has more than seven digits, but is well known for having less than nine.
The legend is that this was originally a counting system of nine digits, but 7, the most feared digit of all, was hungry one evening, and when the rest of the digits woke up they found out that seven ate nine. This is likely apocryphal.
The Yuki language in California and the Pamean languages in Mexico have octal systems because the speakers count using the spaces between their fingers rather than the fingers themselves. The Indians think this is stupid and they just count but ignore thumbs, thus proving that although they may not have invented it, they perfected it.
|
Base 10 - the Decimal System

The basis of the decimal system.
|
Symbols Used
|
| 0 1 2 3 4 5 6 7 8 9
|
| The most popular number base is Base 10. It is often believe that this is due to science following nature, as a marijuana leaf is made up of nine fronds and one stem, giving ten points, and most mathematical concepts and precepts are created while the mathematician is enjoying the effects of excessive marijuana consumption.
By amazing coincidence, the numbers in Base 10 coincide with the numbers we all use for such common tasks as counting peas, children, trees, misfortunes, and marijuana leaves.
By assiduous use of fingers and toes, it has been shown that one can represent almost any quantity of stuff or more of the above digits used in close conjunction with each other. For numbers below the value of the lowest digit, fractions of digits are used, often called "nail clippings."
The Decimal system was invented by American librarian, educator, and humanitarian, Melvil Dewey. However. it appears that he based his inventions on the inventions of the Indian people from many years prior. Nowhere else is this as evident as seen in the comparison of the digits used.
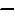 , , 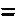 , , 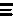 , ,  , ,  , , 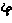 , , 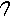 , , 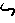 , , 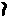
1, 2, 3, 4, 5, 6, 7, 8, 9
See, it's obvious that the Indian system of numerals came first, otherwise why else would the Brahmi (Indian) numerals be on top?
|
Base 12 - the Duodecimal System

The duodecimal numeral system is based on the planet Jupiter.
|
Symbols Used
|
| 0 1 2 3 4 5 6 7 8 9 X E
|
| Base 12 is popularly known as duodecimal. The entire small intestine was named after it. Duodecimal is often regarded as being superior to Base 10. However, people who say that should shut up.
Duodecimal is based around the planet Jupiter and the years it takes to revolve around the Sun. This is unsurprising, giving that the first users of Base 12 are Indians who worshipped the planet as the god "Dyaus pitr."
|
Base 16 - The Hexadecimal System

Modern computers often use hexadecimal numbers.
|
Symbols Used
|
| 0 1 2 3 4 5 6 7 8 9 A B C D E F
|
| Base 16 is popularly known as hexadecimal. The use of the word 'hex' obviously indicates the use of magic in the application of the Base 16 counting system.
When quoting IP address on the Internet Experts often use the Base 10 equivalent of the binary addresses, however when they quote the MAC address of the Computer they often read them in Hex.
When questioned on the reason why, they often say that this is 248. If they didn't do this they would be 57005. What's the problem, are you 57007?
Amongst Internet Experts this is considered high humour. Many Internet Experts come from India. Apparently, this numerical system is starting to 64222 from use.
|
Other number systems
Base I - The ROMAN numeral system

Julius, once head of the ROMAN Empire, trying to work out how they get V to mean five.
|
Symbols Used
|
| I V X L C D M
|
| The ROMAN Numeral system is still extremely popular today by copywriters, as it makes more logical sense to say that a futuristic sci-fi like Return of the Killer Tomatoes! is © MCMLXXXVIII than ©1988.
Rather than deriving value from the more traditional digit placement, Roman Numerals are all of a particular value, so that an I is the equivalent value of 1, V is 5, and so on, as shown below.
- I → 1 V → 5 X → 10 L → 50 C → 100 D → 500 M → 1000
However, when in ROME , always place digits like the ROMANS do. in order to have the number 4, for example, rather than having IIII, the ROMANS have instead chosen to use IV, thus making this a more one I'd system.
Due to the limitations of the system, often numerical suffixes were introduced, most commonly K which represented multiplied by 1,000, to get to numbers higher than one thousand. This was compoundable, so that KK was multiply by 1,000,000. KKK, however, is just absurd.
It was considered high praise to relate to people by numbers instead of names. Caesar, being above most others, was often referred to as 599,000. This practise is still in place today in some motorcycle clubs, so ensure that when you next see a motorcyclist to refer to him as a DICK.
The ROMANS stole all their inventions from the Greeks, who in turn stole all their inventions from the Indians.
|
Base £ - The Imperial system

Leader of the Imperial system
|
Symbols Used
|
| ' yd fath fur in " mi µin mi(naut., U.S., U.K.) rd
|
| Not about to be outdone by the ROMANS, the British Empire also introduced it's own numbering system. The Imperial system is extremely simple to understand. It works on a system of a varying base dependant on what it is you are counting or measuring. As an example the Imperial measurement for length is an inch. Once you have 12 inches you have a foot, and once you have 3 feet you have a yard. Unless of course you were at sea then you had 6.08 feet to a fathom. . Of course, in practise a fathom was actually 2 yards, which was 6 feet. And 100 fathoms made a chain. Unless you were talking about fathoms in practice, which as we said before they were only 6 feet instead of 6.08 feet, as a chain would be 608 feet, which would be 100 true fathoms, or 101.3333 practical fathoms, as this is an easier measurement. Approximately.
And, of course, there is also the link, which is 7.92 inches, or 0.66 of a foot. 25 links would make a pole, which is also known as a rod or a perch. This would mean that a pole would be the equivalent of 5.5 yards, or 2.71382 true fathoms, or 2.75 practical fathoms. And a chain would be 4 perches, or 0.10855 cables, or 792 inches.
Now a furlong is 220 yards, or 660 feet, or 110 practical fathoms, or 108.552632 true fathoms, or 1.085526 chains. But this of course would mean that you would have to be on land. 8 furlongs would make a mile, which would also be the length of 5280 feet, 868.421056 true fathoms, not to be confused with 880 practical fathoms. Of course if you were naughty you would use the nautical mile, which is 6080 feet, or 1000 true fathoms, or 1013.3333 practical fathoms. And a League is 2605.26316 true fathoms, or 240 chains.
And that's just length. The Indians used Imperial measurements during the colonisation by the British. They gave it back.
|
Summary
Obviously the Indians invented every number system, as well as everything to do with numbers. Indians invented Algebra, Differential Calculus, Imaginary numbers, factorials, happy numbers, and magic numbers. In fact, every time that you have ever been given any test in school relating to mathematics there's a strong possibility that it was written by Indians.
When you think about it, Indians are bastards, aren't they?













