Differential Equations

“We do everything in calculus, except backwards...kind of like people in Africa.”

~ Differential Equations on Differential Equations

What is a Differential Equation?

Differential equations have had many different meanings over the course of human history. A few important meanings are universally agreed upon by mathematicians and are listed for your viewing pleasure.

1. Differential equations are not the same. They are different from ordinary equations, just like Uncyclopedia readers. They must be treated with extra care and respect; it is general convention to compliment and caress these special beings while noting that any mention of Down Syndrome will result in your head getting chopped off. Remember, they are different but very "special" too.

2. Differential Equations encompass a more concise set of equations known as indifferent equations. Mostly taught in schools located in the Confederate States of Rednecks (a.k.a Louisville, Kentuckistan), topics covered include Complex eradication of them Yankees, Segregation factors,and Lablack transformations (Transforms a black person white. For instance, Michael Jackson underwent a success Lablack transformation.). Indifferent equations teach students theorems that end in -isms because the existence and uniqueness of those theorems indicate that equations, like people, need to be labeled and differentiated.

3. There is a subtype of differential equations that is so important that it transcends math. These are known as preferential equations. They are solved based on preference (ie. how pretty the equation should look), which naturally opens the entire field of mathematics to girls.

First Order Ordinary Differential Equations (ODEs)

A general differential equation.

To solve any first order ODE, you should do exactly as the ode states. However, for most aspiring mathematicians (and for those guys who devote their love life to screwing numbers), it is virtually impossible to solve an ODE this way--there obviously isn't anything to separate. Most use a parallel axis theorem to accomplish the same goal. Several self-help aids are available online and use the acronym XXX, with each X representing a single derivative of X(t). This method works up to n = 3 for the nth order ODE. Higher order ODEs require the participant to get someone drunk.

While the separation and integration is easily achieved with simple 1st order ODEs, other differential equations are rather prudish and will not separate. These differential equations have been introduced by Jehovah's Witnesses and are universally despised. A new name has also been theorized to properly categorize these equations. In that case, extreme coercion of a legal kind is required to convince the equation to separate. Legal coercion may include the use of chloroform or neurotoxins but never division by zero.

Higher Order Ordinary Differential Equations (HO ODEs)

A.The first equation is the differential equation.
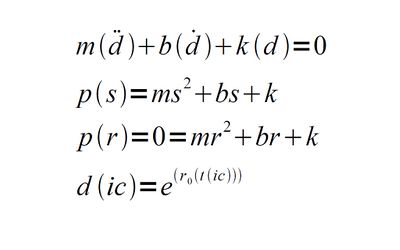
B.The second equation is the characteristic polynomial; note that it is equal to M squared plus bullshit and only differs by a constant every time.
C.The third equation is the root of this polynomial, found by setting p(r) = 0.
D.Then if r sub 0 is a root, you get the fourth equation, the solution to the differential equation. Here time is a function of time. Note that at a time that I See, some very cool stuff happens. This is another reason why math is so fun.

These HO ODEs represent a post-modern view of mathematics that can be compared to Andy Warhol's Factory. Accordingly, there are generally special tricks performed to solve these HO ODEs. However, given that these HO ODEs may sometimes be extremely dangerous to the untrained user, it is recommended that some kind of protection is used.

Here is a general method to performing a solution to a HO ODE:
1. For a homogeneous (ie: common ho ODE), the solution can be found via the method shown on the image to the right.
2. If the roots of the characteristic polynomial equals some positive real number, then the solution will never reach the climax.
3. If the roots of the characteristic polynomial is a negative real number, then the solution will die off. A pitiful transient affair.

Oscillating solutions are used to power steam engines and other biological processes. Double-click to see it in action.

4. If the roots of the characteristic polynomial are imaginary, then the solution will oscillate. If there is some bullshit [bs = 0] happening (ie: you are a terrible problem-solver), then the differential equation will eventually leave you.
5. If there is no bs happening even with imaginary roots, you might as well break out the KY Jelly (a high energy snack) because it is going to be a long night of problem-solving.

Finding a particularly satisfying position to the solution of the differential equation:
Sometimes differential equations are very particular: they will object to performing some types of behavior. This is because there may be initial conditions that limit the range of activities that the equation will perform. For instance, Christian differential equations perform more acts than Islamic differential equations (although no western mathematician has quite dared to venture into the world of Islamic differential equations to provide a rigorous proof of this).

Applications of Differential Equations

There are no applications of differential equations in the real world. No experiment has confirmed the wild fantasies of mathematicians, although the mathematicians were unable to engage in their theoretical work. If there were any applications of differential equations, I guess some of them would be:
1. Sending an input signal, contracting the signal, and pumping the signal back again.
2. Using different damping constants to model the behavior of the gain of the system. An example is massaging a tender body part with skin of different texture and tightness, which has already proven to be a success in many therapies.