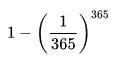Unbirthday problem
In mathematics, the unbirthday problem is the problem of determining the probability that, out of a given set of randomly-selected people, two or more of them share an unbirthday. The problem (as stated) was originally posed by the English mathematician and part-time illegal drug peddler professional photographer Charles L. Dodgson[1].
Definition of "unbirthday"[edit | edit source]
An "unbirthday" is defined as any day of the calendar year which is not the anniversary of a person's day of birth.
Unbirthday probabilities[edit | edit source]
For a typical randomly-selected human, it is assumed that the probability the days of the year of one's unbirthdays is equally distributed throughout the calendar year, ranging from January 1st to December 31st. A particular naive interpretation of this fact would suggest that each unbirthday occurs with a probability of 364/365, or 1-(1/365) (approx. 0.99726027), resulting the probability of a person having at least one unbirthday in a given calendar year to be
or approximately
to 2,000 decimal places.
However, leap days need to be taken into account in such a calculation. In the Gregorian calendar (instituted by King George II in 1752), leap days occur with an average frequency of 97 days per 400 calendar years. In particular, the probability that a randomly selected day is a leap day would be 97/(400 x 365 + 97), or approximately 0.000663942449194713. This makes the average Gregorian year to be increased to 365 + 365 x 0.000663942449194713, for a total of 365.2423389939561 days. Using the Gregorian leap-day correction algorithm, this yields a probability of having a minimum of one unbirthday during the course of a year to be
or
Madness follows[edit | edit source]
It was at this point that Dodgson went blithering mad. After having spent an unproductive 23 years and 37,000 scraps of paper and 29,000 vials of crack working on the inextractable problem, he did not anticipate a solution within his expected lifetime. He therefore gave up and submitted the problem to the London Royal Society of Mathematics in 1873, along with a reward of 350,000 guineas sterling[2] for the first legitimate proof.
The final solution[edit | edit source]
The solution to the problem was finally given less than 30 seconds later, with a correct proof, by Alphonz McStrickly, a lowly copyboy's assistant who was working at the Society's printing press at the time. Unfortunately, Dodgson never considered that the solution hinged on applying the pigeonhole principle (first formalized in 1834 by pigeon fancier Peter G.L. Dirichlet): namely, that it is mathematically impossible to fit more than one pigeon into one pigeonhole. This leads immediately to McStrickly's Lemma[3]:
- McStrickly's Lemma: For any set of two (2) persons, and any three (3) distinct days of the calendar year: if they do not share an unbirthday for any two of those days, then they must share an unbirthday for the remaining day.
or, in formal terms:
It only suffices to eliminate the two remaining degenerate cases of either zero persons, or one person. In either of those extreme cases, there are simply not enough people available to hold a legitimate unbirthday party.
In summary:
| Number of people in the room (n): | Probability that two or more people in that room share an unbirthday (p): |
|---|---|
| 0 | 0 % |
| 1 | 0 % |
| 2 or more | 100 % |
Aftermath[edit | edit source]
Because of his allergy to and innate fear of pigeons, Dodgson was financially ruined by his ill-advised offer and was forced to give up underage erotic photography mathematics and file for bankruptcy. Meanwhile, McStrickly, with the help of his ill-gotten proceeds, became the youngest English schoolboy up to that time to attend London Elementary School (at the age of 19 and a half), and died of cholera three weeks later. Ironically, the day of McStrickly's death was, in fact, his unbirthday.
See also[edit | edit source]